350년만에 풀린 페르마의 마지막 정리
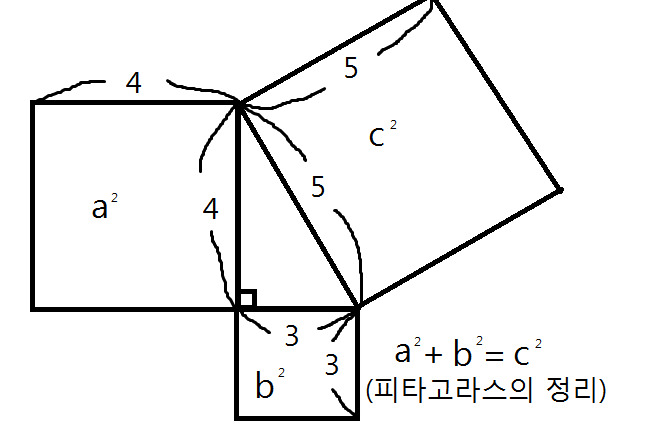
피타고라스의 정리를 모르는 사람은 없을 것이다. 직각삼각형의 가로의 제곱과 세로의 제곱을 더하면 빗변의 제곱이 된다는 사실은 이미 2500년전 피타고라스 때부터 아니 그 이전부터도 알고 있었고 특히 건축에서 긴요하게 활용되어 왔다. 심지어 어떤 목수는 왜 그런지 원리를 모르면서도 자기가 세운 기둥이 직각이 되느냐를 확인하기 위하여 땅에 30cm되는 곳에 점을 찍고 기둥 위에 40cm되는 곳에 점을 찍은 후에 두 점을 연결한 길이가 50cm가 되는가를 보는 것이다.
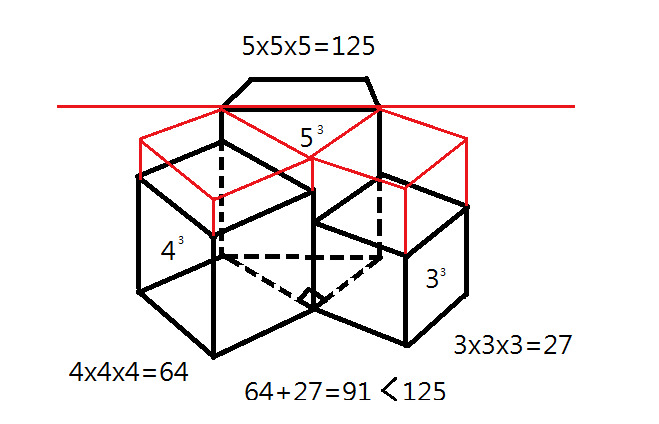
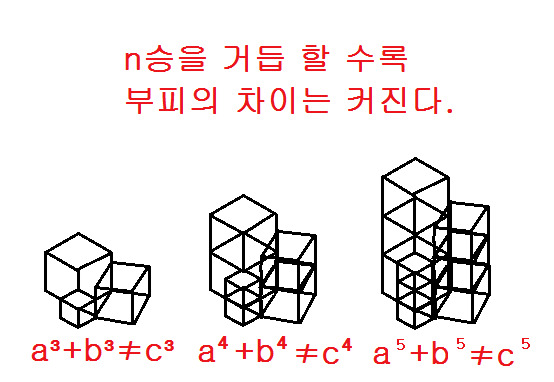
x2 + y2 = z2 의 피타고라스 정리를 만족시키는 x, y, z 3수는 무한이 많이 있다. 그런데 여기서 한발 더 나가서 다음과 같은 발상을 해보자. x3 + y3 = z3 을 만족하는 x, y, z도 있는가 그리고 x4 + y4 =z4 방정식은 해가 있는지 또한 일반식인 xn + yn = zn은 해를 갖고 있는지 등.
원래 법학자로서 법원에 근무하면서 취미로 수학에 몰두했던 피에르 페르마(Pierrede Fermat;1601-1663)는 디오판토스가 쓴 고전의 교본인 산학(Arithmetica)의 사본을 읽다가
a2 + b2 = c2
이라는 피타고라스 방정식과 마주치게 되었다.
그래서 그는 방정식 주변 여백에 다음과 같은 유명한 주석을 썼다.
"방정식 an + bn = cn은 n=2일 경우에만 정수해 a,b,c와 n을 가진다(그러면 이 방정식을 만족하는 무한히 많은 조합의 a,b,c 3중수가 존재한다). 그러나 n>2인 경우에는 해가 없다. 나는 이 명제에 대한 경이적인 증거를 발견했는데, 불행히도 이 책 여백에는 그것을 다 적기에 너무 좁다."
이것을 페르마의 마지막 정리(Fermat's Last Theorem)이다. 이를 가장 엄밀하게 표현하면 다음과 같다.
"xn + yn = zn(n은 3이상의 정수)을 만족하는 정수해 x,y,z는 존재하지 않는다. 단, x,y,z중 하나가 0이거나 모두 0인 경우는 제외한다."
이내용은 페르마가 죽은 후에 그의 아들이 아버지의 수학적업적을 정리하여 책으로 출판한 이후로 수많은 수학자들을 실패와 좌절의 늪으로 넣었다. 1908년에는 "볼프스켈 상" 이 발표되었는데 2007년 9월13일까지 페르마의 정리를 증명하는 사람에게 오늘날 가치로 약 20억원을 상으로 준다는 내용이다. 일평생을 이 수수께끼와 씨름한 사람이 있는가 하면 심지어 너무 고민하다가 스스로 목숨을 끊은 경우의 수학자도 한 두 사람이 아니었다. 많은 수학자들이 증명을 하였다고 큰 소리치다가 발표현장에서 잘못된 점이 지적되거나 아니면 몇일 후에 잘못된 부분이 지적되기도 하였다.
원래부터 어렵다기보다는 사람들이 그것을 증명하기 위한 방법을 못 찾았다고 해야 할 것입니다. 지금도, 오래 전부터 사람들이 시도했지만 풀리지 않은 문제가 많이 있습니다. 간략하게 이 페르마의 마지막 정리에 대해 사람들이 어떤 노력을 해서 어떤 발전이 있었는지 알아 보겠습니다. 페르마 자신은 '직각삼각형의 넓이는 제곱수가 될 수 없다" 즉, x, y, z 가 정수일 때 x2 + y2 = z2 이면, xy/2 는 제곱수가 될 수 없다는 것을 증명했습니다. (페르마가 남긴 글 중 증명이라고는 이것 하나 뿐입니다.) 이것을 사용하면 n 이 4 일 경우는 증명이 됩니다. 그러고 나면, n 이 홀수인 소수일 경우만을 증명하면 된다는 것이 밝혀집니다. 1753년, 오일러(Leonhard Euler)는 자신이 페르마의 마지막 정리를 증명했다고 주장했으나 그 증명에는 오류가 있었습니다. 제르맹(Sophie Germain) 은 페르마의 마지막 정리를 두 경우, 즉
(1) x, y, z 중 어느 것도 n 의 배수가 아닐 때
(2) x, y, z 중 하나만이 n 의 배수일 때
로 나눌 수 있다는 것을 밝히고 100 이하의 n 에 대해 경우 (1)을 증명했습니다. 르장드르(Legendre) 는 제르맹의 방법을 확장하여 197 이하의 n 에 대해 경우 (1)을 증명했습니다.
1825년, 디리클레(Dirichlet) 가 n=5 에 대해 경우 (2)를 증명함으로써 n=5 인 경우의 페르마의 마지막 정리를 증명했습니다.
1832년, 디리클레가 n=14 인 경우의 페르마의 마지막 정리를 증명했습니다. 물론, 이것은 n=7 인 경우를 증명하면 자연히 증명되지만, n=7 인 경우는 증명하지 못했던 것입니다.
1839년, 라메(Lamé)가 n=7 인 경우를 증명했습니다. 그 증명은 너무나 복잡해서 무슨 새로운 접근을 하지 않는 한 더 큰 n 에 대해 증명하는 것은 불가능할 것으로 보였습니다.
1847년, 라메는 페르마의 마지막 정리를 증명했다고 파리 아카데미에 밝혔습니다. 그러나 쿠머(Kummer) 에 의해 37, 59, 67 등의 특수한 경우에는 그 증명을 적용할 수 없다는 것이 밝혀졌습니다. 그 뒤, 쿠머, 미리마노프(Mirimanoff), 비퍼리히(Wieferich), 푸르트뱅글러(Furtwängler), 판디버(Vandiver) 등이 이 특수한 경우들을 하나씩 증명해 냈습니다. 그러나 1915년 옌센(Jensen) 에 의해 이런 특수한 경우들은 무한히 존재한다는 것이 밝혀졌습니다. 그래도 쿠머가 사용했던 방법은 이후 계속 적용되었고, 컴퓨터의 도움을 받아 1993년까지 n 이 40000 이하인 경우는 페르마의 마지막 정리가 참이라는 것이 밝혀졌습니다.
1983년, 폴팅즈(Gerd Faltings) 는, n>2 일 때 xn + yn = zn인 정수는 많아 봐야 유한개라는, 크게 발전된 결과를 내놓았습니다. 그러나 그 "유한개" 라는 것이 모든 n 에 대해 0 이 된다는 결과는 아무래도 나올 것 같지 않았습니다.

마침내, 프린스턴 대학의 와일즈(Andrew Wiles)가 1993년 6월 21일, 22일, 23일에 영국 아이잭 뉴턴 연구소에서 강의하면서 시무라-다니야마-베이유의 추측의 일부를 증명하고, 그것을 적용하여 페르마의 마지막 정리를 증명했습니다. 그러나 12월 4일, 와일즈는 증명에 문제가 있다며 발표를 철회했고, 이듬해인 1994년 Richard Taylor 와 함께 그 문제를 해결하려고 시도했습니다. 그리고 1994년 10월 6일, 와일즈는 세 명의 다른 수학자에게 전해의 증명보다 더 간단해진 새로운 증명을 보내 왔고, 페르마의 마지막 정리는 증명되었습니다.
아무한테도 알리지 않고 7년간 외로운 싸움이라할 수 있는 연구 끝에 발표한 외일즈는 전세계 수학계로부터 쏟아지는 찬사를 받았다. 그의 증명은 여러 분야의 수학적 개념들을 하나로 통합한 "통일된 수학"의 기틀을 마련했다. 페르마의 정리는 현대 수학의 모든 테크닉을 총동원해야만 증명될 수 있는 수학의 정점인 것이다.
그러나 그 후 와일즈의 증명에서 조그만 오류가 발견되었다. 1년간의 또다른 비밀스런 작업이 계속되었지만 와일즈는 날이 갈수록 미궁에 빠져들어갔고 세상사람들은 과거에 수 많은 수학자들이 밟아왔던 길을 와이즈도 걷고 있다고 생각하기에 이르렀다.
사실 와일즈는 그 자신이 7년간 연구하면서 이 사실을 비밀에 부치기 위하여 다른 분야의 논문을 몇 편 미리 써놓고 가끔씩 그 논문들을 발표하여 마치 자기는 페르마의 정리와는 관계없는 연구를 하는 것처럼 위장술을 발휘하였던 것이다. 왜냐하면 와일즈는 그가 연구하는 내용이 세상에 알려지고 마지막 중요한 단계에서 다른 수학자가 몇 년 동안 와일즈가 투자가 시간을 공짜로 벌고 한발 앞서서 최종결과를 발표하여 명예를 독차지하게 될 것을 매우 두려워했기 때문이다. 이러한 생각은 비단 수학자 뿐만 아니라 모든 연구가들에게 있어서 마찬가지 일 것이다. 오류를 해결하려는 또 다른 세월 속에서 지치다가 더 이상 못 견디게 되었을 때 외일즈는 테일러교수를 만났고 둘이서는 서로를 격려해가며 마지막 투혼을 불사르고 있었다.
마침내 와일즈는 평생 잊을 수 없는 환희의 순간을 맞이했다. 그는 계산결과를 약 20분 동안 멍하니 바라보았다고 한다. 드디어 해낸 것이다. 1994년 10월 25일 페르마는 자신이 증명한 "페르마의 마지막 정리", 그리고 동료교수인 리처드 테일러와 함께 증명한 "헤게 대수학의 고리이론적성질" 두 논문을 전자우편으로 공개하였는데 두번째 논문은 첫번째 논문에서의 가장 중요한 부분을 집중적으로 다루었다.

1955년, 다니야마(Yutaka Taniyama) 는 타원함수, 즉 y2 = x3 + ax + b 꼴의 함수에 대해 어떤 문제를 제기했습니다. 시무라(Shimura) 와 베이유(Weil) 는 이 문제를 더 연구하여 하나의 "추측" 을 제기했고 그것은 시무라-다니야마-베이유의 추측이라고 불립니다. 그런데 1984년, 프라이(Gerhard Frey) 는 페르마의 마지막 정리와 시무라-다니야마-베이유의 추측이 서로 관계가 있음을 밝혔고, 1986년에는 리벳(Ken Ribet) 에 의해, 페르마의 마지막 정리에 반례가 있다면 시무라-다니야마-베이유의 추측에도 반례가 생긴다는 것이 증명되었습니다. 즉, 시무라-다니야마-베이유의 추측만 증명하면, 페르마의 마지막 정리가 증명되는 것입니다. 이것으로 페르마의 마지막 정리는 단순히 호기심을 불러일으키는 문제에서, 공간의 기본적인 성질에 관계된 문제로 탈바꿈했습니다. 와일즈(Andrew Wiles) 가 한 일은, 시무라-다니야마-베이유의 추측을, 어떤 일부의 경우에 대해서 증명한 것입니다. 그것으로 페르마의 마지막 정리를 증명하는 데는 충분했던 것입니다.
1908년, 파울 볼프스켄(Paul Wolfsken) 의 유지에 따라 괴팅엔 왕립과학원은 2007년 9월 13일을 기한으로 페르마의 마지막 정리를 증명하는 사람에게 10만 마르크의 상금을 걸었습니다. 이것은 페르마의 마지막 정리에 수많은 사람이 달려들어 잘못된 증명을 쏟아내게하는 한편, 대중에게 이 문제를 널리 알리는 계기가 되었습니다. 1997년 6월 27일, 와일즈는 이 상금을 받았습니다.